by Jochen Szangolies

Aristotle characterized humans as zoon logon echon, the rational animal. In general, we like to believe that our opinions are formed through reason—that we have arrived at them by means of a process of weighing the alternatives, selecting that which we deem most appropriate. This implies a certain mutual intelligibility—I might not share your opinion, but I should be able to appreciate why you hold it.
Yet, with—it seems—increasing frequency, we find ourselves baffled by others’ opinions. Who could, in this day and age, earnestly believe that the Earth is flat? How can a president hold a nearly steady approval rating of over 40%, despite an unprecedented record of lies, scandals, and incompetence?
One might thus conclude that Aristotle somewhat overstated his case. But the issue is more complex: those holding odd beliefs are not typically less intelligent. An answer may be found in the way modern communication media have restructured society, leading to the process of opinion-formation no longer chiefly taking place at the individual, but at the collective level, largely unmoored from concerns of factuality and appropriateness. This is best understood by studying the physics of phase transitions.
Same, but Different
Different phases of a substance are instances where something is the same—yet different. Just think of steam, water, and ice: all three are the same in regards of being H2O, yet they are clearly different in their properties.
Identity is then a notion that depends to some extent on context, and things that appear identical in one respect may prove quite different in others. Moreover, there is a possibility of transitioning between different identities: water may freeze, becoming ice, or boil, becoming steam, all the while remaining H2O. Such conversions are known as phase transitions, and they’re enormously rich phenomena that can be quite tumultuous, even violent—think of a volume of water suddenly being converted into steam: the same mass of H2O occupies a much greater volume as steam than as water, resulting in a steam explosion.
Furthermore, phase transitions are often characterized by discontinuities: quantities that, ordinarily, change smoothly with external parameters like temperature, pressure, or volume, all of a sudden ‘jump’ to different values, disrupting the normally gentle progression from one state to the next.
There are many examples of things being ‘the same, but different’ in everyday life, and not all of them are related to simple physical substances suddenly changing their characteristics after crossing a certain threshold. The concept of phase transition nevertheless may offer us some help in understanding cases where one and the same basic substance may suddenly display different properties. For present purposes, the most interesting application will be to the study of collective opinion-forming in social settings.
Before we can do so, however, we need to take a closer look at what, exactly, phase transitions are, and how and why they occur.
Not just a Phase
Water, like every macroscopic entity, is not a simple substance, but itself a conglomerate of a huge number of more fundamental entities—H2O molecules, as every school child knows today. These can aggregate together in different ways—the rigid crystal lattice of ice, the somewhat looser association of water, and the free-wheeling turbulence of steam. Hence, phases, or states of aggregation, and the transitions between them, are collective phenomena.
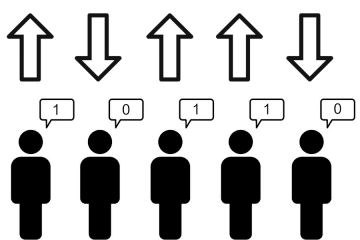
To understand them, we must thus understand how the individual constituents interact. A common model is due to the German physicist Ernst Ising (read: E-zing, not I-zing), and consists of individual systems that can be in two states—‘up’ or ‘down’, +1 or -1—commonly called ‘spins’. Neighboring spins interact in such a way that co-alignment is preferred.
The simplest way to arrange these constituents is in a one dimensional chain. In such a system, a phase transition might be the spontaneous co-alignment of all spins from an initially randomly ordered state.
However, this system does not show any phase transitions: only its two-dimensional generalization does. Thus, not all aggregates serve to demonstrate ‘same, but different’ properties: some can be, in some sense, too simple to do so. In the other direction, this means that adding complexity to a system can transform it from one with smoothly predictable behavior into one that’s susceptible to sudden and disruptive global changes. One might thus find that methods of description and modeling that were apt for a system up to a certain point of complexity suddenly cease to yield good results, once a given threshold is exceeded.
Let us briefly consider a phase transition in the two-dimensional Ising model. Consider a 2D plane of randomly aligned, regularly distributed spins. We can think of this as a ‘high temperature’ situation: the heat applied tends to randomize the spin orientation. As we cool down the system, order will start to emerge: growing ‘patches’—commonly called ‘domains’—of co-aligned spins will form, much like ice floats in zero degree water, and eventually, transition to a totally ordered state, with all spins either pointing up or down.
But wait—what decides the final orientation? The initial state with its random order should not have had any bias towards either direction; yet, a specific, randomly selected direction emerges. This is an example of what’s known as symmetry breaking: there is an underlying symmetry to the system that is no longer present in a certain state. Symmetry breaking is a very powerful notion in physics: for instance, it is at the heart of the Anderson-Higgs mechanism, responsible for mass generation of elementary particles.
The Ising model has, since its inception, found a plethora of applications: from its original goal, finding a model of magnetism, to condensed matter physics, quantum field theory, and more remote areas, such as neuroscience and the modeling of earthquakes. Perhaps most astonishingly, though, is its application in the social sciences: if we think of each spin as a ‘social atom’, with perhaps two distinct opinions on economic policy, it yields a model of how opinions disperse through a population. It’s this application that we turn to now.
Heating Up the Discourse
It may seem surprising that such a simple—indeed, deliberately simplistic—model could have such broad applicability. The reason for this is the notion of universality: the macroscopic dynamics of collective systems decouples from their microscopic details. Thus, any member of a set of such systems yields the same large-scale behavior. Universality is characterized by critical values for certain parameters, such as temperature, and is expressed by the fact that the behavior of these systems upon approaching such critical values (characterized by so-called critical exponents) is the same, no matter the microscopic details.
For the Ising model, very different sorts of behavior emerge above and below the critical temperature, TC.

Figure 3 shows the evolution of the Ising model on a 128 x 128 grid at a temperature of about twice the critical value, for 1000 iterations (all simulations done with this online simulator). We start with a random assignment of values, and let the system run. Due to the finite temperature, at each step, each spin/lattice site has a chance to flip its value.
In a social setting, we might think about this as follows: each color, black or white, represents a certain opinion; opinions change, for instance, when an individual comes into contact with new information. By and large, when we encounter which information, and whether we find it convincing, can be regarded as a random process.
We see that after some time, there is some clustering: black and white is less evenly distributed. This is due to the interaction of the spins: roughly speaking, people tend to have similar opinions as their closest associates. Overall, however, the relative amount of black and white—the overall ‘magnetization’ m—will tend to stay constant on average, fluctuating, in the example, around the zero value.
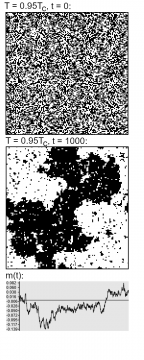
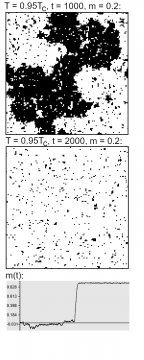
Figure 4, now, shows the case of a temperature just slightly below the critical one (0.95 TC). There, large-scale zones of equal orientation/color form over time: similar opinions cluster strongly together. However, the overall magnetization still averages out to approximately zero (although for low temperatures and long times, we will eventually observe spontaneous net magnetization). If we think of black as ‘prefers Party A’, and white as ‘prefers Party B’, a vote would not show any obvious discrepancy between the two cases. But then, does it really make that much of a difference?
There are, in fact, crucial qualitative differences between the above- and below-TC cases. A first hint of this is offered in Figure 5. There, the difference between two successive steps in the two cases is shown: these are the spins that flipped from one step to the next—that changed their opinion, so to speak. Crucially, below the critical temperature, much fewer flips happen—individuals more rarely change their opinion. This can be explained by noting that in case of large-scale clustering, many more spins are surrounded by spins of the same orientation; hence, it will be much harder to get any individual spin to flip.
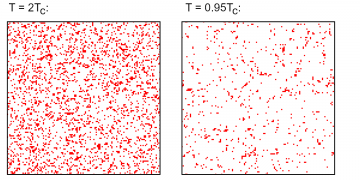
Consequently, in a clustered phase, people tend to stick with their opinion: an argument, a fact, a piece of evidence that might have succeeded in convincing them in the high-temperature case, may fail to do so below the critical value. While the two phases thus may be the same regarding the prevalence of certain opinions, they are different in regards to how strongly these opinions are held, and for which reasons.
It isn’t immediately clear what, exactly, is meant by ‘temperature’, here. What does it mean to cool down, or heat up, a system composed of communicating people? However, we can dodge this issue: rather than thinking about the temperature changing, we can keep it constant, and instead increase the influence each spin exerts on its neighbors. (Mathematically, the reason for this is that the probability for one spin to flip goes as e-J/T, with J being the strength of the interaction; increasing this has the same effect as decreasing T.)
This ‘coupling’ strength, however, has a more readily available interpretation: it is essentially the amount of communication between individuals. Increasing this amount of communication then amounts to decreasing the effective temperature; thus, our modern, communication-heavy society should be considered to be at a lower ‘temperature’ than earlier societies with fewer channels of communication, and every increase in communication should be considered to further lower this temperature. Social media might thus have a quite chilling effect on our discourse.
There is another effect of modern communication media: where in the past, communication would mostly occur on the one-on-one-level, we now have the ability to effectively communicate with large numbers of people simultaneously. Thus, what was once a one-dimensional chain akin to a game of telephone has become a highly interconnected network—which, as discussed above, may thus be more prone to showing phase transitions.
If this is right, then, in a communication-heavy society, opinion-formation is more highly influenced by social factors than by a consideration of facts on the level of the individual. It becomes less important what the reasons are for some opinion to be held, and more who else holds this opinion. This means that attempts to change individual minds—presenting facts, data, evidence—will be less effective; the facts and arguments are no longer among the chief factors determining opinion. Opinions become decoupled from their factual basis.
In one way, this is perhaps a relief: it isn’t that people at large have become less rational, but simply the change of the locus of opinion-formation from the individual to the collective, brought on by the prevalence of communication in modern society. But on the other hand, this is clearly a dangerous development: how do we change a mind that’s made up not thanks to a process of deliberation, but due to collective dynamics? No amount of debunking, say, the lies of a politician will sway their committed base, because belief in these lies is not the reason for their commitment.
Indeed, this threatens one of the key assumptions of democracy: that the will of the collective arises as an amalgamation of individual preferences. In a strongly-coupled society, things are rather inverted: the opinion of the individual is the result of the dynamics at the level of the collective—which, as with the direction of magnetization of a magnet, may ultimately be little more than random.
But there is a yet more worrying feature of systems in a clustered phase: they are much more vulnerable towards external influences. Consider, as an example, switching on a magnetic field, which will tend to align the spins in a preferred direction.
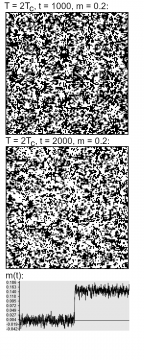
In Figure 6, the reaction of a weakly-coupled ‘society’ is shown. As is to be expected, we find some resulting magnetization—a higher fraction of white-colored sites. Some event—perhaps a bit of news, a scandal, or the rise of a prominent voice—has led to one of the options being preferred: an overall normal turn of events.
Things are different with the strongly-coupled system, however. In Figure 7, the same magnetic field is applied—but the reaction is much more drastic: almost all the spins will align, leading to near-total magnetization. The externally-imbued opinion becomes dominant, to near extinction of all alternatives.
The tendency towards clustering reinforces the effect of the external field, and the domains of spins oriented along this direction expand, ultimately merging.
But what could be the cause of such an ‘external field’? Well, in the domain of political factions, it might be the rise of a ‘strongman’, providing an unquestionable source of truth—that is, a society in a ‘clustered’ phase may be a society vulnerable towards authoritarianism, more eager and willing to fall into lockstep with party discipline than one in which political opinion is predominantly decided at the individual level.
In this way, the increased frequency and amount of communication due to modern media, social and otherwise, as well as the higher complexity (‘dimensionality’) of the resulting structure, may have played a critical role in driving current society away from a healthy market of opinion. A tendency towards clustering leads to facts and arguments being less effective at swaying individual opinion, the propagation of ‘alternative facts’ and derisive cries of ‘fake news’; thus, collective opinion becomes decoupled from factual reality, entering into a sui generis realm where what’s actually what counts little. Moreover, the global rise of authoritarianism may be an effect of the vulnerability of strongly-coupled societies against external, destabilizing influences. Ultimately, collective opinions may even arise spontaneously—akin to spontaneous magnetization—trumping individual reason.
Of course, this is a radically simplified model. We are not little spins taking one of two states, but complex individuals with rich inner lives. Furthermore, each of us communicates in different ways, with different individuals—a better model of the structure of our communication might be a graph with nodes connected in different ways. But still, thanks to universality, there is a chance that the above might have an important lesson to teach—one we should take into account when taking stock of our own opinions.
Most of us are aware, to some degree, of the biases and flaws of reasoning that may lead the individual to form a skewed opinion; but the influence of the collective on individual opinion is perhaps less appreciated. It takes energy to form our own opinions, to defend our stance against those closest to us—it is much easier, and psychologically rewarding, to fall in line. But sometimes, this is energy worth investing: not just for our own sake, but also, for that of society at large.
