by Ashutosh Jogalekar

Progress in science often happens when two or more fields productively meet. Astrophysics got a huge boost when the tools of radio and radar met the age-old science of astronomy. From this fruitful marriage came things like the discovery of the radiation from the big bang. Another example was the union of biology with chemistry and quantum mechanics that gave rise to molecular biology. There is little doubt that some of the most important future discoveries in science in the future will similarly arise from the accidental fusion of multiple disciplines.
One such fusion sits on the horizon, largely underappreciated and unseen by the public. It is the fusion between physics, computer science and biology. More specifically, this fusion will likely see its greatest manifestation in the interplay between information theory, thermodynamics and neuroscience. My prediction is that this fusion will be every bit as important as any potential fusion of general relativity with quantum theory, and at least as important as the development of molecular biology in the mid 20th century. I also believe that this development will likely happen during my own lifetime.
The roots of this predicted marriage go back to 1867. In that year the great Scottish physicist James Clerk Maxwell proposed a thought experiment that was later called ‘Maxwell’s Demon’. Maxwell’s Demon was purportedly a way to defy the second law of thermodynamics that had been proposed a few years earlier. The second law of thermodynamics is one of the fundamental laws governing everything in the universe, from the birth of stars to the birth of babies. It basically states that left to itself, an isolated system will tend to go from a state of order to one of disorder. A good example is how a bottle of perfume wafts throughout a room with time. This order and disorder was quantified by a quantity called entropy.
In technical terms, the order and disorder refers to the number of states a system can exist in; order means fewer states and disorder means more. The second law states that isolated systems will always go from fewer states and lower entropy (order) to more states and higher entropy (disorder). Ludwig Boltzmann quantified this relationship with a simple equation carved on his tombstone in Vienna: S = klnW, where k is a constant called the Boltzmann constant, ln is the natural logarithm (to the base e) and W is the number of states.
Maxwell’s Demon was a mischievous creature which sat on top of a box with a partition in the middle. The box contains molecules of a gas which are ricocheting in every direction. Maxwell himself had found that these molecules’ velocities follow a particular distribution of fast and slow. The demon observes these velocities, and whenever there is a molecule moving faster than usual in the right side of the box, he opens the partition and lets it into the left side, quickly closing the partition. Similarly he lets in slower moving molecules from left to right. After some time, all the slow molecules will be in the right side and the fast ones will in the left. Now, velocity is related to temperature, so this means that one side of the box has heated up and the other has cooled down. To put it another way, the box went from a state of random disorder to order. According to the second law this means that the entropy of the system of the system decreased, which is impossible.
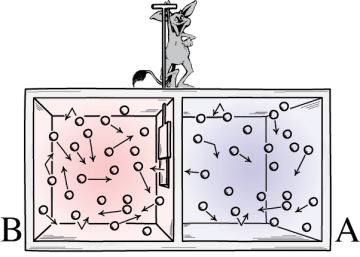
For the next few years scientists tried to get around Maxwell’s Demon’s paradox, but it was in 1922 that the Hungarian physicist Leo Szilard made a dent in it when he was a graduate student hobnobbing with Einstein, Planck and other physicists in Berlin. Szilard realized an obvious truth that many others seem to have missed. The work and decision-making that the demon does to determine the velocities of the molecules itself generates entropy. If one takes this work into account, it turns out that the total entropy of the system has indeed increased. The second law is safe. Szilard later went on to a distinguished career as a nuclear physicist, patenting a refrigerator with Einstein and becoming the first person to think of a chain reaction.
Perhaps unknowingly, however, Szilard had also discovered a connection – a fusion of two fields – that was going to revolutionize both science and technology. When the demon does work to determine the velocities of molecules, the entropy that he creates comes not just from the raising and lowering of the partition but from his thinking processes, and these processes involve information processing. Szilard had discovered a crucial and tantalizing link between entropy and information. Two decades later, mathematician Claude Shannon was working at Bell Labs, trying to improve the communication of signals through wires. This was unsurprisingly an important problem for a telephone and communications company. The problem was that when engineers were trying to send a message over a wire, it would lose its quality because of many factors including noise. One of Shannon’s jobs was to figure out how to make this transmission more efficient.
Shannon found out that there is a quantity that relates to the information transmitted over the wire. In crude terms, this quantity was inversely related to the information as well as to the probability of transmitting that information; the higher the probability of transmitting accurate information over a channel, the lower this quantity was and vice versa. When Shannon showed his result to the famous mathematician John von Neumann, von Neumann with his well-known lightning-fast ability to connect disparate ideas, immediately saw what it was: “You should call your function ‘entropy’”, he said, “firstly because that is what it looks like in thermodynamics, and secondly because nobody really knows what entropy is, so in a debate you will always have the upper hand.” Thus was born the connection between information and entropy. Another fortuitous connection was born – between information, entropy and error or uncertainty. The greater the uncertainty in transmitting a message, the greater the entropy, so entropy also provided a way to quantify error. Shannon’s 1948 paper, “A Mathematical Theory of Communication”, was a seminal publication and has been called the Magna Carta of the information age.
Even before Shannon, another pioneer had published a paper that laid the foundations of the theory of computing. In 1936 Alan Turing published “On Computable Numbers, with an Application to the Entscheidungsproblem”. This paper introduced the concept of Turing machines which also process information. But neither Turing nor von Neumann really made the connection between computation, entropy and information explicit. Making it explicit would take another few decades. But during those decades, another fascinating connection between thermodynamics and information would be discovered.

That connection came from Stephen Hawking getting annoyed. Hawking was one of the pioneers of black holes, and along with Roger Penrose he had discovered that at the center of every black hole is a singularity that warps spacetime infinitely. The boundary of the black hole is its event horizon and within that boundary not even light can escape. But black holes posed some fundamental problems for thermodynamics. Every object contains entropy, so when an object disappears into a black hole, where does its entropy go? If the entropy of the black hole does not increase then the second law of thermodynamics would be violated. Hawking had proven that the area of a black hole’s event horizon never decreases, but he had pushed the thermodynamic question under the rug. In 1972 at a physics summer school, Hawking met a graduate student from Princeton named Jacob Bekenstein who proposed that the increasing area of the black hole was basically a proxy for its increasing entropy. This annoyed Hawking and he did not believe it because increased entropy is related to heat (heat is the highest- entropy form of energy) and black holes, being black, could not radiate heat. With two colleagues Hawking set out to prove Bekenstein wrong. In the process, he not only proved him right but also made what is considered his greatest breakthrough: he gave black holes a temperature. Hawking found out that black holes do emit thermal radiation. This radiation can be explained when you take quantum mechanics into account. The Hawking-Bekenstein discovery was a spectacular example of another fusion: between information, thermodynamics, quantum mechanics and general relativity. Hawking deemed it so important that he wanted to put it on his tombstone in Westminster Abbey, and so it has been.
This short digression was to show that more links between information, thermodynamics and other disciplines were being forged in the 1960s and 70s. But nobody saw the connections between computation and thermodynamics until Rolf Landauer and Charles Bennett came along. Bennett and Landauer were both working at IBM. Landauer was an émigré who fled from Nazi Germany before working for the US Navy as an electrician’s mate, getting his PhD at Harvard and joining IBM. IBM was then a pioneer of computing; among other things they had built computers for the Manhattan Project. In 1961, Landauer published a paper titled “Irreversibility and Heat Generation in the Computing Process” that is destined to become a classic of science. In it, Landauer established that the basic act of computation – the change of one bit to another, say a 1 to a 0 – requires a bare minimum amount of entropy. He quantified this amount with another simple equation: S = kln2, with k again being the Boltzmann constant and ln the natural logarithm. This has become known as the Landauer bound; it is the absolute minimum amount of entropy that has to be expended in a single bit operation. Landauer died in 1999 and as far as I know the equation is not carved on his tombstone.
The Landauer bound applies to all kinds of computation in principle and biological processes are also a form of information processing and computation, so it’s tantalizing to ask whether Landauer’s calculation applies to them. Enter Charles Bennett. Bennett is one of the most famous scientists whose name you may not have heard of. He is not only one of the fathers of quantum computing and quantum cryptography but he is also one of the two fathers of the marriage of thermodynamics with computation, Landauer being the other. Working with Landauer in the 1970s and 80s, Bennett applied thermodynamics to both Turing machines and biology. By good fortune he had gotten his PhD in physical chemistry studying the motion of molecules, so his background primed him to apply ideas from computation to biology.

To simplify matters, Bennett considered what he called a Brownian Turing machine. Brownian motion is the random motion of atoms and molecules. A Brownian Turing machine can write and erase characters on a tape using energy extracted from a random environment. This makes the Brownian Turing machine reversible. A reversible process might seem strange, but in fact it’s found in biology all the time. Enzyme reactions occur from the reversible motion of chemicals – at equilibrium there is equal probability that an enzymatic reaction will go forward or backward. What makes these processes irreversible is the addition of starting materials or the elimination of chemical products. Even in computation, only a process which erases bits is truly irreversible because you lose information. Bennett envisaged a biological process like protein translation as a Brownian Turing machine which adds or subtracts a molecule like an amino acid, and he calculated the energy and entropy expenditures involved in running this machine. Visualizing translation as a Turing machine made it easier to do a head-to-head comparison between biological processes and bit operations. Bennett found out that if the process is reversible the Landauer bound does not hold and there is no minimum entropy required. Real life of course is irreversible, so how do real-life processes compare to the Landauer bound?
In 2017, a group of researchers published a fascinating paper in the Philosophical Transactions of the Royal Society in which they explicitly calculated the thermodynamic efficiency of biological processes. Remarkably, they found that the efficiency of protein translation is several orders of magnitude better than the best supercomputers, in some cases as better as a million fold. More remarkably, they found that the efficiency is only one order of magnitude worse than the theoretical minimum Landauer bound. In other words, evolution has done one hell of a job in optimizing the thermodynamic efficiency of biological processes.
But not all biological processes. Circling back to the thinking processes of Maxwell’s little demon, how does this efficiency compare to the efficiency of the human brain? Surprisingly, it turns out that neural processes like the firing of synapses are estimated to be much worse than protein translation and more comparable to the efficiency of supercomputers. At first glance, the human brain thus appears to be worse than other biological processes. However, this seemingly low computational efficiency of the brain must be compared to its complex structure and function. The brain weighs only about a fiftieth of the weight of an average human but it uses up 20% of the body’s energy. It might seem that we are simply not getting the biggest bang for our buck, with an energy-hungry brain providing low computational efficiency. What would explain this inefficiency and this paradox?
My guess is that the brain has been designed to be inefficient through a combination of evolutionary accident and design and that efficiency is the wrong metric for gauging the performance of the brain. Efficiency is the wrong metric because thinking of the brain in digital terms is the wrong metric. The brain arose through a series of modular inventions responding to new environments created by both biology and culture. We now know that thriving in these environments needed a combination of analog and digital functions.; for instance, the nerve impulses controlling blood pressure are digital while the actual change in pressure is continuous and analog. It is likely that digital neuronal firing is built on an analog substrate of wet matter, and that higher-order analog functions could be emergent forms of digital neuronal firing. As early as the 1950s, von Neumann conjectured that we would need to model the brain as both analog and digital in order to understand it. Around the time that Bennett was working out the thermodynamics of computation, two mathematicians named Marian Pour-El and Ian Richards proved a very interesting theorem which showed that in certain cases, there are numbers that are not computable with digital computers but are computable with analog processes; analog computers are thus more powerful in such cases.
If our brains are a combination of digital and analog, it’s very likely that they are this way so that they can span a much bigger range of computation. But this bigger range would come at the expense of inefficiency in the analog computation process. The small price of lower computational efficiency as measured by the Landauer bound would come at the expense of the much greater evolutionary benefits of performing complex calculations that allow us to farm, build cities, know stranger from kin and develop technology. Essentially, the Landauer bound could be evidence for the analog nature of our brains. There is another interesting fact about analog computation, which is its greater error rate; digital computers took off precisely because they had low error rates. How does the brain function so well in spite of this relatively high error rate? Is the brain consolidating this error when we dream? And can we reduce this error rate by improving the brain’s efficiency? Would that make our brains better or worse at grasping the world?
From the origins of thermodynamics and Maxwell’s Demon to the fusion of thermodynamics with information processing, black holes, computation and biology, we have come a long way. The fusion of thermodynamics and computation with neuroscience just seems to be beginning, so for a young person starting out in the field the possibilities are exciting and limitless. A multitude of general questions abound: How does the efficiency of the brain relate to its computational abilities? What might be the evolutionary origins of such abilities? What analogies between the processing of information in our memories and that in computers might we discover through this analysis? And finally, just like Shannon did for information, Hawking and Bekenstein did for black holes and Landauer and Bennett did for computation and biology, can we find out a simple equation describing how the entropy of thought processes relates to simple neural parameters connected to memory, thinking, empathy and emotion? I do not know the answers to these questions, but I am hoping someone who is reading this will, and at the very least they will then be able to immortalize themselves by putting another simple formula describing the secrets of the universe on their tombstone.
Further reading:
- Charles Bennett – The Thermodynamics of Computation
- Seth Lloyd – Ultimate Physical Limits to Computation
- Freeman Dyson – Are brains analog or digital?
- George Dyson – Analogia: The Emergence of Technology Beyond Programmable Control (August 2020)
- Richard Feynman – The Feynman Lectures on Computation (Chapter 5)
- John von Neumann – The General and Logical Theory of Automata
