by Ashutosh Jogalekar
 In November 1918, a 17-year-student from Rome sat for the entrance examination of the Scuola Normale Superiore in Pisa, Italy’s most prestigious science institution. Students applying to the institute had to write an essay on a topic that the examiners picked. The topics were usually quite general, so the students had considerable leeway. Most students wrote about well-known subjects that they had already learnt about in high school. But this student was different. The title of the topic he had been given was “Characteristics of Sound”, and instead of stating basic facts about sound, he “set forth the partial differential equation of a vibrating rod and solved it using Fourier analysis, finding the eigenvalues and eigenfrequencies. The entire essay continued on this level which would have been creditable for a doctoral examination.” The man writing these words was the 17-year-old’s future student, friend and Nobel laureate, Emilio Segre. The student was Enrico Fermi. The examiner was so startled by the originality and sophistication of Fermi’s analysis that he broke precedent and invited the boy to meet him in his office, partly to make sure that the essay had not been plagiarized. After convincing himself that Enrico had done the work himself, the examiner congratulated him and predicted that he would become an important scientist.
In November 1918, a 17-year-student from Rome sat for the entrance examination of the Scuola Normale Superiore in Pisa, Italy’s most prestigious science institution. Students applying to the institute had to write an essay on a topic that the examiners picked. The topics were usually quite general, so the students had considerable leeway. Most students wrote about well-known subjects that they had already learnt about in high school. But this student was different. The title of the topic he had been given was “Characteristics of Sound”, and instead of stating basic facts about sound, he “set forth the partial differential equation of a vibrating rod and solved it using Fourier analysis, finding the eigenvalues and eigenfrequencies. The entire essay continued on this level which would have been creditable for a doctoral examination.” The man writing these words was the 17-year-old’s future student, friend and Nobel laureate, Emilio Segre. The student was Enrico Fermi. The examiner was so startled by the originality and sophistication of Fermi’s analysis that he broke precedent and invited the boy to meet him in his office, partly to make sure that the essay had not been plagiarized. After convincing himself that Enrico had done the work himself, the examiner congratulated him and predicted that he would become an important scientist.
Twenty five years later Fermi was indeed an important scientist, so important in fact that J. Robert Oppenheimer had created an entire division called F-Division under his name at Los Alamos, New Mexico to harness his unique talents for the Manhattan Project. By that time the Italian emigre was the world’s foremost nuclear physicist as well as perhaps the only universalist in physics – in the words of a recent admiring biographer, “the last man who knew everything”. He had led the creation of the world’s first nuclear reactor in a squash court at the University of Chicago in 1942 and had won a Nobel Prize in 1938 for his work on using neutrons to breed new elements, laying the foundations of the atomic age.
The purpose of F-division was to use Fermi’s unprecedented joint abilities in both experimental and theoretical physics to solve problems that stumped others. To Fermi other scientists would take their problems in all branches of physics, many of them current or future Nobel laureates. They would take advantage of Fermi’s startlingly simple approach to problem-solving, where he would first qualitatively estimate the parameters and solution and then plug in complicated mathematics only when necessary to drive relentlessly toward the solution. He had many nicknames including “The Roadroller”, but the one that stuck was “The Pope” because his judgement on any physics problem was often infallible and the last word.
Fermi’s love for semi-quantitative, order-of-magnitude estimates gave him an unusual oeuvre. He loved working out the most rigorous physics theories as much as doing back-of-the-envelope calculations designed to test ideas; the latter approach led to the famous set of problems called ‘Fermi problems‘. Simplicity and semi-quantitative approaches to problems are the hallmark of models, and Fermi inevitably became one of the first modelers. Simple models such as the quintessential “spherical cow in a vacuum” are the lifeblood of physics, and some of the most interesting insights have come from using such simplicity to build toward complexity. Interestingly, the problem that the 17-year-old Enrico had solved in 1918 would inspire him in a completely novel way many years later. It would be the perfect example of finding complexity in simplicity and would herald the beginnings of at least two new, groundbreaking fields.
Los Alamos was an unprecedented exercise in bringing a century’s worth of physics, chemistry and engineering to bear on problems of fearsome complexity. Scientists quickly realized that the standard tools of pen and paper that they had been using for centuries would be insufficient, and so for help they turned to some of the first computers in history. At that time the word “computer” meant two different things. One meaning was women who calculated. The other meaning was machines which calculated. Women who were then excluded from most of the highest echelons of science were employed in large numbers to perform repetitive calculations on complicated physics problems. Many of these problems at Los Alamos were related to the tortuous flow of neutrons and shock waves from an exploding nuclear weapon. Helping the female computers were some of the earliest punched card calculators manufactured by IBM. Although they didn’t know it yet, these dedicated women working on those primitive calculators became history’s first pioneering programmers. They were the forerunners of the women who worked at NASA two decades later on the space program.
Fermi had always been interested in these computers as a way to speed up calculations or to find new ways to do them. At Los Alamos a few other far-seeing physicists and mathematicians had realized their utility, among them the youthful Richard Feynman who was put in charge of a computing division. But perhaps the biggest computing pioneer at the secret lab was Fermi’s friend, the dazzling Johnny von Neumann, widely regarded as the world’s foremost mathematician and polymath and fastest thinker. Von Neumann who had been recruited by Oppenheimer as a consultant because of his deep knowledge of shock waves and hydrodynamics had become interested in computers after learning that a new calculating machine called ENIAC was being built at the University of Pennsylvania by engineers J. Presper Eckert, John Mauchly, Herman Goldstine and others. Von Neumann realized the great potential of what we today call the shared program concept, a system of programming that contains both the instructions for doing something and the process itself in the same location, both coded in the same syntax.
 Fermi was a good friend of von Neumann’s, but his best friend was Stanislaw Ulam, a mathematician of stunning versatility and simplicity who had been part of the famous Lwów School of mathematics in Poland. Ulam belonged to the romantic generation of Central European mathematics, a time during the early twentieth century when mathematicians had marathon sessions fueled by coffee in Lwów, Vienna and Warsaw’s famous cafes, where they scribbled on the marble tables and argued mathematics and philosophy late into the night. Ulam had come to the United States in the 1930s; by then von Neumann had already been firmly ensconced at Princeton’s Institute for Advanced Study with a select group of mathematicians and physicists including Einstein. Ulam had started his career in the most rarefied parts of mathematics including set theory; he later joked that during the war he had to stoop to the level of manipulating actual numbers instead of merely abstract symbols. After the war started Ulam had wanted to help with the war effort. One day he got a call from Johnny, asking him to a move to a secret location in New Mexico. At Los Alamos Ulam worked closely with von Neumann and Fermi and met the volatile Hungarian physicist Edward Teller with whom he began a fractious, consequential working relationship.
Fermi was a good friend of von Neumann’s, but his best friend was Stanislaw Ulam, a mathematician of stunning versatility and simplicity who had been part of the famous Lwów School of mathematics in Poland. Ulam belonged to the romantic generation of Central European mathematics, a time during the early twentieth century when mathematicians had marathon sessions fueled by coffee in Lwów, Vienna and Warsaw’s famous cafes, where they scribbled on the marble tables and argued mathematics and philosophy late into the night. Ulam had come to the United States in the 1930s; by then von Neumann had already been firmly ensconced at Princeton’s Institute for Advanced Study with a select group of mathematicians and physicists including Einstein. Ulam had started his career in the most rarefied parts of mathematics including set theory; he later joked that during the war he had to stoop to the level of manipulating actual numbers instead of merely abstract symbols. After the war started Ulam had wanted to help with the war effort. One day he got a call from Johnny, asking him to a move to a secret location in New Mexico. At Los Alamos Ulam worked closely with von Neumann and Fermi and met the volatile Hungarian physicist Edward Teller with whom he began a fractious, consequential working relationship.
Fermi, Ulam and von Neumann all worked on the intricate calculations involving neutron and thermal diffusion in nuclear weapons and they witnessed the first successful test of an atomic weapon on July 16th, 1945. All three of them realized the importance of computers, although only von Neumann’s mind was creative and far-reaching enough to imagine arcane and highly significant applications of these as yet primitive machines – weather control and prediction, hydrogen bombs and self-replicating automata, entities which would come to play a prominent role in both biology and science fiction. After the war ended, computers became even more important in the early 1950s. Von Neumann and his engineers spearheaded the construction of a pioneering computer in Princeton. After the computer achieved success in doing hydrogen bomb calculations at night and artificial life calculations during the day, it was shut down because the project was considered too applied by the pure mathematicians. But copies started springing up at other places, including one at Los Alamos. Partly in deference to the destructive weapons whose workings would be modeled on it, the thousand ton Los Alamos machine was jokingly christened MANIAC, for Mathematical Analyzer Numerical Integrator and Computer. It was based on the basic plan proposed by von Neumann which is still the most common plan used for computers worldwide – the von Neumann architecture.
After the war, Enrico Fermi had moved to the University of Chicago which he had turned into the foremost center of physics research in the country. Among his colleagues and students there were T. D. Lee, Edward Teller and Subrahmanyan Chandrasekhar. But the Cold War imposed on his duties, and the patriotic Fermi started making periodic visits to Los Alamos after President Truman announced in 1951 that he was asking the United States Atomic Energy Commission to resume work on the hydrogen bomb as a top priority. Ulam joined him there. By that time Edward Teller had been single-mindedly pushing for the construction of a hydrogen bomb for several years. Teller’s initial design was highly flawed and would have turned into a dud. Working with pencil and paper, Fermi, Ulam and von Neumann all confirmed the pessimistic outlook for Teller’s design, but in 1951, Ulam had a revolutionary insight into how a feasible thermonuclear weapon could be made. Teller honed this insight into a practical design which was tested in November 1952, and the thermonuclear age was born. Since then, the vast majority of thermonuclear weapons in the world’s nuclear arsenals have been based on some variant of the Teller-Ulam design.
By this time Fermi had acutely recognized the importance of computers, to such an extent in fact that in the preceding years he had taught himself how to code. Work on the thermonuclear brought Fermi and Ulam together, and in 1955 Fermi proposed a novel project to Ulam. To help with the project Fermi recruited a visiting physicist named John Pasta who had worked as a beat cop in New York City during the Depression. With the MANIAC ready and standing by, Fermi was especially interested in problems where highly repetitive calculations on complex systems could take advantage of the power of computing. Such calculations would be almost impossible in terms of time to perform by hand. As Ulam recalled later,
“Fermi held many discussions with me on the kind of future problems which could be studied through the use of such machines. We decided to try a selection of problems for heuristic work where in the absence of closed analytic solutions experimental work on a computing machine might perhaps contribute to the understanding of properties of solutions. This could be particularly fruitful for problems involving the asymptotic, long time or “in the large” behavior of non-linear physical systems…Fermi expressed often a belief that future fundamental theories in physics may involve non-linear operators and equations, and that it would be useful to attempt practice in the mathematics needed for the understanding of non-linear systems. The plan was then to start with the possibly simplest such physical model and to study the results of the calculation of its long-term behavior.”
Fermi and Ulam had caught the bull by its horns. Crudely speaking, linear systems are systems where the response is proportional to the input. Non-linear systems are ones where the response can vary disproportionately. Linear systems are the ones which many physicists study in textbooks and as students. Non-linear systems include almost everything encountered in the real world. In fact, the word “non-linear” is highly misleading, and Ulam nailed the incongruity best: “To say that a system is non-linear is to say that most animals are non-elephants.” Non-linear systems are the rule rather than the exception, and by 1955 physics wasn’t really well-equipped to handle this ubiquity. Fermi and Ulam astutely realized that the MANIAC was ideally placed to attempt a solution to non-linear problems. But what kind of problem would be complex enough to attempt by computer, yet simple enough to provide insights into the workings of a physical system? Enter Fermi’s youthful fascination with vibrating rods and strings.
The simple harmonic oscillator is an entity which physics students encounter in their first or second year of college. Its distinguishing characteristic is that the force applied to it is proportional to the displacement. But as students are taught, this is an approximation. Real oscillators – real pendulums, real vibrating rods and strings in the real world – are not simple. The force applied results in a complicated function of the displacement. Fermi and Ulam set up a system consisting of a string attached to one end. They considered four models; one where the force is proportional to the displacement, one where the force is proportional to the square of the displacement, one where it’s proportional to the cube, and one where the displacement varies in a discontinuous way with the force, going from broken to linear and back. In reality the string was modeled as a series of 64 points all connected through these different forces. The four graphs from the original paper are shown below, with force on the x-axis and displacement on the y-axis and the dotted line indicating the linear case.
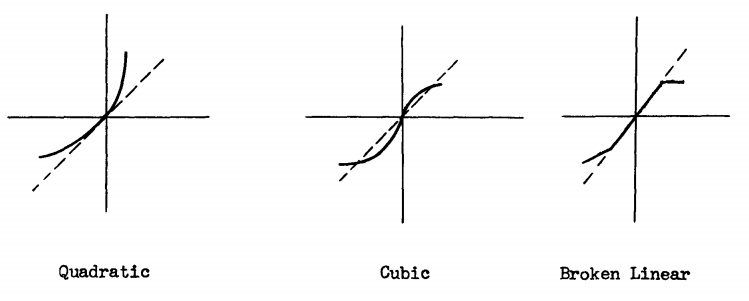
Here’s what the physicists expected: the case for a linear oscillator, familiar to physics students, is simple. The string shows a single sinusoidal node that remains constant. The expectation was that when the force became non-linear, higher frequencies corresponding to two, three and more sinusoidal modes would be excited (these are called harmonics or overtones). The global expectation was that adding a non-linear force to the system would lead to an equal distribution or “thermalization” of the energy, leading to all modes being excited and the higher modes being heavily so.
What was seen was something that was completely unexpected and startling, even to the “last man who knew everything.” When the quadratic force was applied, the system did indeed transition to the two and three-mode system, but the system then suddenly did something very different.
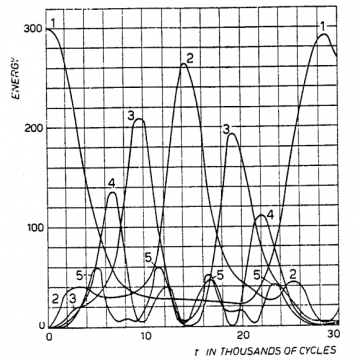
“Starting in one problem with a quadratic force and a pure sine wave as the initial position of the string, we indeed observe initially a gradual increase of energy in the higher modes as predicted. Mode 2 starts increasing first, followed by mode 3 and so on. Later on, however, this gradual sharing of energy among successive modes ceases. Instead, it is one or the other mode that predominates. For example, mode 2 decides, as it were, to increase rather rapidly at the cost of all other modes and becomes predominant. At one time, it has more energy than all the others put together! Then mode 3 undertakes this role.”
Fermi and Ulam could not resist adding an exclamation point even in the staid language of scientific publication. Part of the discovery was in fact accidental; the computer had been left running overnight, giving it enough time to go through many more cycles. The word “decides” is also interesting; it’s as if the system seems to have a life of its own and starts dancing of its own volition between one or two lower modes; Ulam thought that the system was playing a game of musical chairs. Finally it comes back to mode 1, as if it were linear, and then continues this periodic behavior. An important way to describe this behavior is to say that instead of the initial expectation of equal distribution of energy among the different modes, the system seems to periodically concentrate most or all of its energy in one or a very small number of modes. The following graph for the quadratic case makes this feature clear: on the y-axis is energy while on the x-axis is the number of cycles ranging into the thousands (as an aside, this very large number of cycles is partly why it would be impossible to solve this problem using pen and paper in reasonable time). As is readily seen, the height of modes 2 and 3 is much larger than the higher modes.
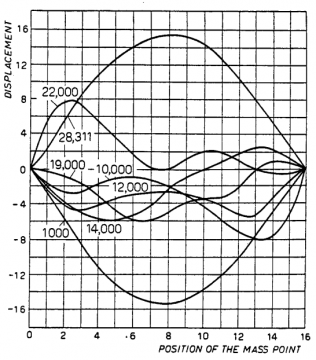
The actual shapes of the string corresponding to this asymmetric energy exchange are even more striking, indicating how the lower modes are disproportionately excited. The large numbers here again correspond to the number of cycles.
The graphs for the cubic and broken displacement case are similar but even more complex, leading to higher modes being excited more often but the energy still concentrated into the lower modes. Needless to say, these results were profoundly unexpected and fascinating. The physicists did not quite know what to make of them, and Ulam found them “truly amazing”. Fermi told him that he thought they had made a “little discovery”.
The 1955 paper contains an odd footnote: “We thank Ms. Mary Tsingou for efficient coding of the problems and for running the computations on the Los Alamos MANIAC machine.” Mary Tsingou was the underappreciated character in the story. She was a Greek immigrant whose family barely escaped Italy before Mussolini took over. With bachelor’s and master’s degrees in mathematics from Wisconsin and Michigan, in 1955 she was a “computer” at Los Alamos, just like many other women. Her programming of the computer was crucial and non-trivial, but she was acknowledged in the work and not in the writing. She worked later with von Neumann on diffusion problems, was the first FORTRAN programmer, and even did some calculations for Ronald Reagan’s infamous “Star Wars” program. As of 2020, Mary Tsingou is still alive and 92 and living in Los Alamos. The Fermi-Pasta-Ulam problem should be called the Fermi-Pasta-Ulam-Tsingou problem.
Fermi’s sense of having made a “little discovery” has to be one of the great understatements of 20th century physics. The results that he, Ulam, Pasta and Tsingou obtained went beyond harmonic systems and the MANIAC. Until then there had been two revolutions in 20th century physics that changed our view of the universe – the theory of relativity and quantum mechanics. The third revolution was quieter and started with French mathematician Henri Poincare who studied non-linear problems at the beginning of the century. It kicked into high gear in the 1960s and 70s but still evolved under the radar, partly because it spanned several different fields and did not have the flashy reputation that the then-popular fields of cosmology and particle physics had. The field went by several names, including “non-linear dynamics”, but the one we are most familiar with is chaos theory.
As James Gleick who gets the credit for popularizing the field in his 1987 book says, “Where chaos begins, classical science stops.” Classical science was the science of pen and pencil and linear systems. Chaos was the science of computers and non-linear systems. Fermi, Ulam, Pasta and Tsingou’s 1955 paper left little reverberations, but in hindsight it is seminal and signals the beginning of studies of chaotic systems in their most essential form. Not only did it bring non-linear physics which also happens to be the physics of real world problems to the forefront, but it signaled a new way of doing science by computer, a paradigm that is the forerunner of modeling and simulation in fields as varied as climatology, ecology, chemistry and nuclear studies. Gleick does not mention the report in his book, and he begins the story of chaos with Edward Lorenz’s famous meteorology experiment in 1963 where Lorenz discovered the basic characteristic of chaotic systems – acute sensitivity to initial conditions. His work led to the iconic figure of the Lorenz attractor where a system seems to hover in a complicated and yet simple way around one or two basins of attraction. But the 1955 Los Alamos work got there first. Fermi and his colleagues certainly demonstrated the pull of physical systems toward certain favored behavior, but the graphs also showed how dramatically the behavior would change if the coefficients for the quadratic and other non-linear terms were changed. The paper is beautiful. It is beautiful because it is simple.
It is also beautiful because it points to another, potentially profound ramification of the universe that could extend from the non-living to the living. The behavior that the system demonstrated was non-ergodic or quasiergodic. In simple terms, an ergodic system is one which visits all its states given enough time. A non-ergodic system is one which will gravitate toward certain states at the expense of others. This was certainly something Fermi and the others observed. Another system that as far as we know is non-ergodic is biological evolution. It is non-ergodic because of historical contingency which plays a crucial role in natural selection. At least on earth, we know that the human species evolved only once, and so did many other species. In fact the world of butterflies, bats, humans and whales bears some eerie resemblances to the chaotic world of pendulums and vibrating strings. Just like these seemingly simple systems, biological systems demonstrate a bewitching mix of the simple and the complex. Evolution seems to descend on the same body plans for instance, fashioning bilateral symmetry and aerodynamic shapes from the same abstract designs, but it does not produce the final product twice. Given enough time, would evolution be ergodic and visit the same state multiple times? We don’t know the answer to this question, and finding life elsewhere in the universe would certainly shed light on the problem, but the Fermi-Pasta-Ulam-Tsingou problem points to the non-ergodic behavior exhibited by complex systems that arise from simple rules. Biological evolution with its own simple rules of random variation, natural selection and neutral drift may well be a Fermi-Pasta-Ulam-Tsingou problem waiting to be unraveled.
The Los Alamos report was written in 1955, but Enrico Fermi was not one of the actual co-authors because he had tragically died in November 1954, the untimely consequence of stomach cancer. He was still at the height of his powers and would have likely made many other important discoveries compounding his reputation as one of history’s greatest physicists. When he was in the hospital Stan Ulam paid him a visit and came out shaken and in tears, partly because his friend seemed so composed. He later remembered the words Crito said in Plato’s account of the death of Socrates: “That now was the death one of the wisest men known.” Just three years later Ulam’s best friend Johnny von Neumann also passed into history. Von Neumann had already started thinking about applying computers to weather control, but in spite of the great work done by his friends in 1955, he did not realize that chaos might play havoc with the prediction of a system as sensitive to initial conditions as the global climate. It took only seven years before Lorenz found that out. Ulam himself died in 1984 after a long and productive career in physics and mathematics. Just like their vibrating strings, Fermi, Ulam and von Neumann had ascended to the non-ergodic, higher modes of the metaphysical universe.
Further reading:
- Studies of Non-linear Problems. E. Fermi, J. Pasta and S. Ulam, Document LA-1940, May 1955.
- Fermi, Pasta, Ulam and a Mysterious Lady, T. Dauxois, Physics Today, January 2008
- Adventures of a Mathematician, S. M. Ulam, 1976
