by Jonathan Kujawa

Each year my department hosts an all-day event for high school students interested in math. Nowadays we have approximately 400 students and 20-30 teachers join us from all across Oklahoma and north Texas. Some drive 2+ hours each way to come!
The students’ goal? Probably getting out of class is high on the list :-).
Our goal is for the students to have fun and see interesting math they are likely to have never seen before. More generally we hope the students see math as a lively, engaging, and creative subject with lots of interesting open questions which are areas of active research. It’s meant to be an antidote to the dusty, rigid, cut-and-dry subject they usually see in an educational system focused on standardized tests and the like.

The highlight of the day, at least for me, is a talk by a visiting mathematician chosen for their reputation as an excellent speaker. It gives me an all-to-rare chance to hear a non-technical introduction to some cool math. This year we had the pleasure of hosting Diana Davis. Dr. Davis earned her Ph.D. from Brown University in 2013 and is now faculty at Swarthmore College. She gave a fantastic talk about playing billiards on a pentagonal billiard table.
Since we are mathematicians who are untroubled by the real world, we will always assume there is no friction nor spin to our billiard balls. This means the angle of incidence equals the angle of reflection and a ball can bounce around the table forever. We’ll also assume the table has no pockets and the ball never hits a corner. This is because our interest will be in understanding the trajectories a ball could take as it bounces around the table and pockets and corners would cause complications. A fundamental first question is if there is always a periodic trajectory: that is, a path that eventually repeats itself and, hence, repeats over and over forever.
On a rectangular table, it isn’t hard to see if you shoot the bar directly towards the opposite side, then it will bounce back and forth forever between the far and near walls. Thinking a little harder, you see you can also angle a shot so that it bounces off each wall in turn so the ball travels in a closed cycle:
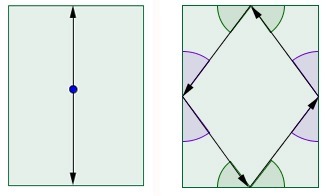

Of course, a boring back-and-forth trajectory is still possible on this table, but what about more interesting ones? Or, even better, what about periodic trajectories on more exotic shapes, like Dr. Davis’s pentagons? The good news is that in 1986 Howard Masur proved any polygon whose angles are rational multiples of π have infinitely many periodic trajectories. In fact, Drs. Boshernitzan, Galperin, Kruger, and Troubetzkoy proved in this case the periodic trajectories are dense among all trajectories. Roughly speaking, dense means while your favorite trajectory might not repeat itself, you only need to very slightly tweak the position of the ball or angle of your shot to make it periodic.
Masur’s theorem is simply great and it opens the door to all sorts of interesting questions. How many trajectories are there? Can we describe them? How long can they go before they repeat? What happens for other shapes?
Before we talk about more exotic tables, we should first think about an ordinary square. On a square table it turns out to be not so hard to prove a trajectory is periodic if and only if the slope of the initial shot (that is, the rise/run if you draw the starting trajectory on a square piece of paper) is a fraction. Amazingly we can do even better. If the slope is the fraction a/b and where we’ve canceled any common factors out of a and b, then the number of times the ball will bounce off a wall before it starts repeating its path is exactly 2(a+b). If your starting shot has slope 17/3, then the ball will endlessly repeat the same path and it will bounce off 40 walls during one transit of the cycle.
The next easiest table should be the triangle — after all, it has only three sides. Very close readers of 3QD will recall we came across the problem of billiards on triangular tables way back in 2014. Which triangular tables admit periodic trajectories? As mentioned there, it’s known that every billiard table which is an acute triangle (i.e., one in which all three angles are less than 90 degrees) has a starting trajectory that gives a periodic orbit. This was already known to Fagnano in 1775.
Even to do this day it remains an open question what happens for billiards on an obtuse triangle. Back in 2014, the most we could say was the result of Richard Schwartz from 2006 which shows every triangle with no angle larger than 100 degrees has a periodic trajectory. However, just last year Tokarsky, Garber, Marinov, and Moore proved every triangular table with no angle larger that 112.3 degrees has a periodic trajectory. Both their proof and Dr. Schwartz involves a mixture of mathematics and computer calculations. It is still an open question if there is always a periodic trajectory on the even more obtuse triangles.
And of course we have no idea how to describe which trajectories are periodic in a triangle like we can with the a/b result for square tables. It is not so hard to give a classification of the periodic paths in an equilateral triangle. For example, this was done in a 2007 Baxter and Umble paper. Part of what makes this case (and the square) easier is the fact you can tile the plane with equilateral triangles. This lets you “unfold” a trajectory and instead think of it as a path on the plane. This simplifies things greatly. On the other hand, it looks to be extremely hard to describe the periodic trajectories for more general triangles.
If triangles are hard, maybe we should think about pentagons? To make our lives easier, we’ll only consider the regular pentagon where all five angles and all five sides are identical. With a nice regular shape like this, maybe we can make some progress. This is where Dr. Davis comes in. She studies, among other things, periodic orbits on such billiard tables [2].
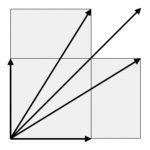
If you were to try to tile the plane with pentagons you would fail as the tiles are forced to overlap. Nevertheless, you can do a more sophisticated version of “unfolding” trajectories trick. In this case the unfolding leads to the Golden L, an L-shaped table made of a 1 x 1 square and two 1 x (1/φ) rectangles. Here φ is short for the golden ratio. If you were to calculate, the slopes of the three lines in the middle of the picture are 1/φ, 1, and φ. Moreover, notice that these lines divide the Golden L into four regions.
Drs. Davis and Lelièvre show that the periodic paths in the regular pentagon can be matched one-to-one with sequences of finite length s1, s2, s3, s4, …., sn where each si corresponds to one of these four regions [4]. That is, given such a sequence you can compute a periodic trajectory, and given a periodic trajectory you can compute the corresponding sequence.
Moreover, using this sequence it isn’t hard to compute something they call the “long saddle connection vector” [a+bφ, c+dφ]. The beauty of this guy is it tells you that the number of wall bounces your ball takes on one transit of the cycle. It makes exactly 10(a+b+c+d) bounces in one cycle [5].
You might think that giving a description of all the periodic trajectories is the end of the line. Hardly! It’s just the beginning! With such a description you can now ask to explore the “space” of periodic trajectories on the pentagon. For example, you can randomly “walk” through this space by randomly choosing a sequence of regions on the Golden L. You can ask what properties such a randomly chosen trajectory might have. Alternatively, you can make deliberate choices in order to discover hidden beauty and structure.
For example, by making a deliberate choice of regions, Drs. Davis and Lelièvre constructed the periodic trajectory at the top of the page. This is one with 1460 wall bounces and you’ll see it covers some regions of the pentagon much more heavily than others. This preference for certain regions over others is quite strange and it is extremely unlikely you’d discover it by random search.
Or, you can just search pentagonal billiard space for beautiful trajectories:

You can find the first 512 periodic trajectories on the regular pentagon here on Dr. Davis’s homepage.
In fact, by popular demand, Dr. Davis made earrings from some of the more popular trajectories. I don’t know if she has any available to purchase, but it wouldn’t hurt to ask. After all, it is the gift-giving season!
[1] Image borrowed from here.
[2] It might not surprise you to hear that her Ph.D. advisor was none other than Richard Schwartz. It also has to be mentioned that Dr. Davis won the Math/Physics category for Dance your Ph.D.!
[3] Image is from the paper by Drs. Davis and Lelièvre. As far as I know, the L-shaped table at the Adam and Eve pub is not a Golden L, but I may have to take a field trip the next time I’m in London for research purposes.
[4] This seems like a strange way to describe the periodic trajectories, but there is a similar description for the square which just happens to match up with the fractions a/b we talked about earlier. Geometrically this description is very natural (it has to do with shear mappings) and, in particular, more easily translates to non-square settings.
[5] In truth, there are a few exceptional cases where it only makes 5(a+b+c+d) or 2(a+b+c+d) bounces, but they tell us exactly when those occur.
