by Jonathan Kujawa
 Last time we found ourselves discussing the topic of writing numbers in different bases. We happen to like base 10 thanks to our ten figures and ten toes, but base 2 (binary), base 16 (hexidecimal), and base 60 (sexagesimal: thanks, Babylonians!) are also often used. But those are human preferences. Math don’t care. If you’ve got twelve Honey badgers, it doesn’t matter if you write it as 12, 1100, c, or as an eye looking at two trees, you’ve got the same number of problems in your life. There may be philosophical quandaries about what exactly is the number “twelve”, or if it exists in its own right or not. But it isn’t controversial to say how you choose to write twelve has little to nothing to do with twelveness.
Last time we found ourselves discussing the topic of writing numbers in different bases. We happen to like base 10 thanks to our ten figures and ten toes, but base 2 (binary), base 16 (hexidecimal), and base 60 (sexagesimal: thanks, Babylonians!) are also often used. But those are human preferences. Math don’t care. If you’ve got twelve Honey badgers, it doesn’t matter if you write it as 12, 1100, c, or as an eye looking at two trees, you’ve got the same number of problems in your life. There may be philosophical quandaries about what exactly is the number “twelve”, or if it exists in its own right or not. But it isn’t controversial to say how you choose to write twelve has little to nothing to do with twelveness.
 It’s rather like changing fonts. Not many would say a change of font will make a parking ticket sting less (although Comic Sans might make it sting more). As endless internet discussions rage about the meaning and content of the Mueller report, altogether too few dissect Robert Mueller’s choice of fonts [1].
It’s rather like changing fonts. Not many would say a change of font will make a parking ticket sting less (although Comic Sans might make it sting more). As endless internet discussions rage about the meaning and content of the Mueller report, altogether too few dissect Robert Mueller’s choice of fonts [1].
But mathematicians leave no stone unturned. Even if nearly every rock is just a rock, every so often you find a geode. One thing math teaches us is the value of persistent questioning. After all, when we talked about the Exploding Dots we found if you turn bases this way and that, you discover you can also use 2/3 and other fractions as bases! This time we’ll find ourselves studying knots before we know it.
In the last essay, we touched on Edray Goins’s recent paper on which numbers are palindromes in base 10 as well as in a different base. In some ways you might think this result is more amusing than profound. After all, being a palindrome arguably doesn’t tell you much about a number, and being a palindrome in some base is arguably more of a coincidence than anything. What is striking about Dr. Goins’s result is that even though there are infinitely many palindromes in any single base, there are only finitely many palindromes in base 10 and a second base. On the other hand, palindromes are a vanishingly small fraction of all numbers. So perhaps it would be even more surprising if were otherwise.
Pursuing this line of thinking, it is reasonable to think if a number has a certain property when you write it in any choice of base, then that property must be a Fundamental Truth about the number. For example, consider the rational numbers. We learn in school that the rational numbers are those which can be written as the ratio of two integers (like 3/4, -17/8, 2/341, …). These are pretty reasonable numbers. After all, I know what it means to have 2/341 of a cake for dessert.
One way to say the rational numbers are manageable is the fact that you only need a finite amount of information to store, comprehend, and compute with them. I only need the string of digits 2, 3, 4, and 1 along with the knowledge of where to draw the / to capture the entirety of 2/341. Another way to frame the finitude of a rational number is the fact we learn in school that the rational numbers are precisely the real numbers which when you write them down (in base 10, natch) eventually terminate or start repeating themselves over and over in an endless loop. Either way, they are precisely the real numbers which can be written down using finitely many digits in base 10.
In fact, the rational numbers are precisely the real numbers which can be written down using finitely many digits in any base! This seems to match our philosophy that something which is true in all bases is a Fundamental Truth. Being describable in a finite amount of information sure feels like an intrinsic property of a number, doesn’t it?
In contrast, irrational numbers like √2 and π run on forever without any discernable pattern when written in any base. Indeed, both √2 and π are thought to be normal numbers. While widely believed, this is still an open problem.
 A normal number is one where if you randomly select a string of digits from the written form of that number, then all strings of that length are equally likely. For example, a 7 is as likely as a 3, a 34 is as likely as a 92, a 1212121212 is as likely as an 8161847617, and so on. Roughly speaking, being normal means you have no discernable patterns at any size scale. Pretty much the exact opposite of being describable with a finite amount of information!
A normal number is one where if you randomly select a string of digits from the written form of that number, then all strings of that length are equally likely. For example, a 7 is as likely as a 3, a 34 is as likely as a 92, a 1212121212 is as likely as an 8161847617, and so on. Roughly speaking, being normal means you have no discernable patterns at any size scale. Pretty much the exact opposite of being describable with a finite amount of information!
In fact, to be normal we require that it have this property when written in any base. Keeping with our philosophy, being a normal number seems to be a Fundamental Truth. In particular, this suggests √2 is a very long ways from being rational. While I can draw the √2 as the diagonal of a one by one square, writing it down using finitely many digits seems a fool’s errand.
Incidentally, since no rational number is normal and we know of numbers which are normal in base 10 but not in another base, it might seem being normal is very, very rare. Quite the opposite! More than a century ago Émile Borel proved nearly all numbers are normal [2]. Despite this, we pretty much still can’t write down a single actual example of a normal number. The real numbers are a terrifying wilderness.
When a stone won’t crack under blows to one side, perhaps it’s worth attacking from another direction. What happens if we revisit our assumptions about what it means to write down a number? Recall, writing a number in base 10, say, is about writing it as a sum using the powers of 10. For example, 42.312 is shorthand for 4(10)+2(1) + 3(1/10)+1(1/100)+2(1/1000). Changing base only changes the 10 for another number. The mathematical operation is still addition. Since subtraction is just addition by a negative, perhaps we can safely pass it over [3].
On the other hand, multiplication and division are operations we might want to take seriously as an alternative. Much as subtraction is to addition, multiplication is to division. We chose to focus on dividing. Is it possible to write numbers as successive divisions instead of additions? Yep. As we’ll soon see, we can write them as continued fractions.
Here is how continued fractions work. Given any number bigger than 1, we can always split it into the part before the decimal point and the part after the decimal point. For example, 42.312 = 42 + 312/1000. In math, anything worth doing once is worth doing over and over. Using the simple trick
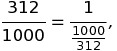
we set ourselves up to split again. Namely, since 1000/312 = 3 + 6/312 we can plug this in, flip the fraction, and do it again, and again, and again…
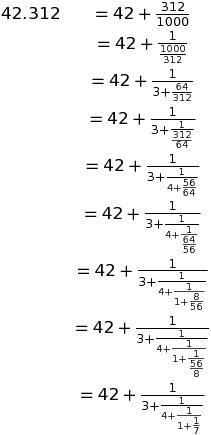
Every real number can be written as a sequence of repeated divisions in this fashion. Of course, there is no law which says it will ever stop. But we have this problem with addition as well. Writing π as sum of powers of 10 requires us to go on forever, after all. These are exactly the digits of its decimal form.
Since writing teetering towers of fractions quickly gets tiring, just like in sums where we only write the digits, we do the same for fractions. Using this shorthand, the repeated fraction for 42.312 is [42, 3, 4, 1, 7].
We’ve already agreed the rational numbers are special in any base. Are they special as partial fractions? On the one hand, if you have a partial fraction which terminates after finitely many steps it is not hard to see you can use algebra to simplify and write it as a single fraction. That is, every finite partial fraction is a rational number. On the other hand, using the division algorithm (aka long division from school) it is only a little more difficult to see the partial fraction of any rational number will terminate. This matches with our expectation that the rational numbers can be captured with a finite amount of information.
 However, something funny soon happens. Our favorite irrational number is √2. However, when you write it as a partial fraction you get [1,2,2,2,2,2,2,2,2,…], with the 2 repeating forever! Remember, it is generally believed √2 is a normal number. It is expected to show no patterns at any scale in any base. Mysteriously and miraculously, partial fractions allow us to capture all the rationals and more with a finite amount of information. The Golden Ratio, (1+√5)/2, (another favorite irrational number) has partial fraction [1,1,1,1,1,…].
However, something funny soon happens. Our favorite irrational number is √2. However, when you write it as a partial fraction you get [1,2,2,2,2,2,2,2,2,…], with the 2 repeating forever! Remember, it is generally believed √2 is a normal number. It is expected to show no patterns at any scale in any base. Mysteriously and miraculously, partial fractions allow us to capture all the rationals and more with a finite amount of information. The Golden Ratio, (1+√5)/2, (another favorite irrational number) has partial fraction [1,1,1,1,1,…].
Don’t forget, all we are doing is writing numbers in a different way. It should seem no more exotic than changing the base (after all, all we did was switch from addition to division). So which numbers can be written as repeating partial fractions? In the 18th century, Joseph-Louis Lagrange proved the striking theorem that a real number can be written as a repeating partial fraction if and only if it is the zero of ax²+bx+c where a, b, and c are integers. This matches with our examples since √2 and the Golden Ratio are both essentially square roots and, indeed, both are a zero of such a quadratic polynomial.
There is one other number worth mentioning. Euler’s constant:
e = 2.71828182845904523536028747135266249775724709369995…
is another famous irrational number. It appears in lots of places, including any time you have exponential growth or decay. It is another one of those numbers which everyone believes is a normal number but nobody can prove. Yet, despite supposedly being equally random at all size scales, the partial fraction of e has an easy to remember pattern:
e=[2,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,…].
Perhaps not surprisingly, writing numbers as partial fractions is a useful tool when studying questions in number theory. After all, this the part of math which studies the properties of numbers.
Much more surprisingly, there is a connection to knot theory! Knot theory is exactly what it sounds like. It is the study of the mathematics of knots. As we discussed here at 3QD several years ago, the study of knots started with Lord Kelvin’s theory of atomic vortices but then took on a life of its own. It is now a rich and active area of math research with connections to string theory, protein folding, vortices in fluid flow, and all sorts of useful things. The most difficult problem in knot theory is to effectively tell if two knots are equal to each other or not, where knots are considered equal if you can transform one into the other by pushing and stretching strands around without cutting, untying, gluing, or otherwise damaging the string.
An interesting class of knots is the rational knots. These are ones which can be made from two pieces of string which have been knotted together by twisting the strands as many times as you like, alternating between the vertical and horizontal directions. Here is an example of a rational knot [4]:
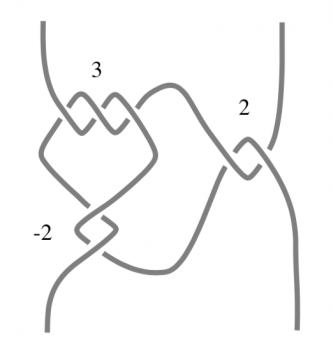
The numbers tell you how many twists there are and the positive or negative sign depends on if the twist is clockwise or counterclockwise. Rational knots give an interesting family of knots and they show up in many of the real world places knot theory can be applied.
In the late 1960s John Conway introduced rational knots and showed one can read off a partial fraction from them. In the example above, the partial fraction is [2,-2,3]. Even better, Conway proved the absolutely amazing theorem that two rational knots are equivalent if and only if they have the same partial fraction! Given that some of the deepest results in knot theory can barely tell if a complicated tangle is equivalent to an unknotted string, or not, this is an astonishing result. If you happen to know you’re starting with a rational knot, this easy to calculate number will tell you exactly which knot you have!
Once again relentless curiosity and a willingness to keep chipping away reveals hidden treasure.

[1] It’s not zero, though! Here is an essay divining meaning from the fact the Mueller report is written in Times New Roman and uses two spaces after every period.
[2] “Normal number” is a terrible name. Mathematicians all too often seem irresistibly drawn to uninspiring terminology. But at least in this case, it is apt: Borel showed us it is normal for a number to be a normal number.
[3] This is a huge mistake, as it happens. When you think about adding and subtracting numbers, if you push hard enough, you find yourself in the mysterious world of conditionally convergent series. We touched on these strange creatures five years ago.
[4] Image borrowed from this paper by Kauffman and Lambropoulou.
