by Jonathan Kujawa
If you believe Sheldon Cooper, physicists have a working knowledge of the universe. Mathematicians aren’t so humble. We like to think we aren’t constrained by reality. As is usually the case, xkcd put it well:

Mathematicians like to think they are able to transcend time and space at will with a stick of chalk as their only weapon. Of course, the truth is we are all limited in what we can grasp. As John von Neumann famously said: “In mathematics you don’t understand things. You just get used to them.” von Neumann was being deliberately provocative but he was also telling the truth.
Even when we think we are on solid mathematical ground our footing can easily be shaken by a small shift in point of view. Whether we make a deliberate decision or not, how we choose to observe and record determines what we can see and understand. There is an important distinction to be drawn in math and in life between things which depend on our viewpoint and those which don’t.
We saw a hint last time here at 3QD. We discovered the humble real numbers which we know and love from our school days are a vast and ultimately unknowable universe. The overwhelming majority of them will be forever out of reach. Even so we find real numbers comfortingly familiar. Even if we don’t understand them, we’ve gotten used to them.
We probably feel pretty okay with the integers. Having 14 banjos or owing someone 3 pineapples is not hard to grasp. Fractions aren’t much worse as we can imagine having 2/3 of a cake or 5/2 (aka 2 and 1/2) apple pies. Even some irrational numbers are pretty down to earth. After all, √2 is nothing but the distance between opposite corners of a 1 by 1 square, and π is the distance around a circle which has diameter 1. Even better, check out my favorite new example of π in an unexpected place: it counts how many times a small block bounces between a much larger block and a wall.
In any case, real numbers aren’t so scary, right? And contrary to my warning, it certainly seems we haven’t made any consequential decisions about how we study them. They are what they are. After all, real numbers are just long (and potentially infinite) strings of digits. Isn’t π just 3.1415926535…?
Even in writing down a number we have made consequential choices. If we write 2019 we have already decided at least two things: we are writing our numbers using sums and using base 10. Writing 2019 is shorthand for 2(1000) + 0(100)+1(10)+9(1). That is, reading right to left, 2019 tells us we should add nine 1’s (=100), one 10 (=101), zero 100’s (=102), and two 1000;s (=103). That is, we group things by 1’s, 10’s, 100’s, 1,000’s, 10,000’s, etc. Going left to right on the right side of the decimal point you do the same but using 1/10, 1/100, 1/1000,… For example, 42.312 is whatever you get when you calculate 4(10)+2(1) + 3(1/10)+1(1/100)+2(1/1000).
Even though we all learn this in elementary school, I wanted to remind you because I think most people (myself included!) have it so ingrained we forget there is a distinction between what we write and the number itself. As von Neumann might say, we’ve gotten so used to it we forget there is something to understand.

After all, there nothing special about 10 here [1]. Sure, we have 10 figures and 10 toes. When sloths rule the world, we’ll probably use powers of 6 instead. Then 42 = 4(6)+2(1) will be what we write when someone asks us how many letters there are in the English alphabet [2]. The number you choose to use when writing your numbers is called your base.
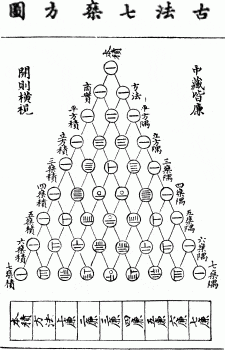
Some mathematical questions are about intrinsic properties of the numbers themselves. If you have three apples and someone gives you another eight apples, you now have eleven apples, regardless of how you write it in your apple ledger. Whether or not a number can be written as a product of two others does not depend on how you choose to write them. You can recognize Pascal’s triangle, even when it is written in fourteenth-century Chinese:
On the other hand, there are questions which do depend on how you write your numbers. For example, you could ask if a number is a palindrome or not when you write it down. In base 10, 212 is a palindrome. In base 6 it is 552 (=5(36)+5(6)+2(1)). Whether or not it is a palindrome depends on your choice of base.
Of course, palindromes on their own aren’t very interesting. You can easily write them all in a list. But mathematicians never leave a stone unturned. If you play with palindromes for a bit you’ll discover 141 in base 10 is 353 in base 6. Both humans and sloths would agree that this number should be called a palindrome. Further messing around shows 207702 in base 10 is 625526 in base 8.
This raises a much more interesting question: Which numbers are a palindrome when written using base 10 and also when written using another base?

I recently ran across a fun paper by Edray Goins [3] from 2009 which answered a narrower question: which numbers are a palindrome when written using base 10 and also when written using another base, and in both cases use exactly the same number of digits? Since 141 and 353 both have three digits, this is an example of what we are looking for (as are 207702 and 625526 as they both have six digits).
Dr. Goins proves there are exactly 203 numbers which are palindromes with two digits or more in base 10 and also palindromes with the same number of digits in another base. The smallest is 22, which is 11 in base 21. The largest is 9986831781362631871386899, which is 101758752109333910257857101 in base 11. In fact, Dr. Goins gives a complete list of all such palindromes. Curiously, the second base is almost always 11, 9, or some other number close to our first base 10 [4].
Surprisingly, there has been very little work done on palindromes. For example, instead of requiring one of the bases to be 10, you could ask instead for numbers which are palindromes in any two bases. Or, as Dr. Goins asks at the end of his paper, you could ask which number is a palindrome for the most different bases?
If you want to be really transgressive, you don’t have to limit yourself to 2, 3, 4, 5,…. as possible bases. Last year we talked about James Tanton’s Exploding Dots. Playing with those you discover you can just as easily have a base of 2/3 or 7/5 or whatever ratio you prefer. Crazy!
Now is the perfect time to think about these sorts of questions. Not surprisingly, Dr. Goins’s paper depends on a computer search for palindromes. With modern computers, there are discoveries just waiting to be made!
Lest you forget, there was actually two choices to be made when writing down numbers. The second was that we would use base 10, but the first was that we would use addition to combine the individual groups. But this isn’t the only option. You can instead use division. This leads to the amazing world of continued fractions, but that will have to wait until next time.
[1] The Babylonians liked to group things into 60 for the very sensible reason that 60 can be easily subdivided into 2’s, 5’s, 6’s, 10’s, 12’s, 20’s, 30’s etc. while 10 is much more limited. Thanks to them we have sixty minutes in an hour and 360 degrees in a full circle.
[2] Presuming, of course, our sloth overlords allow for English :-).
[3] Dr. Goins is also the subject of a recent New York Times article and a thought-provoking essay about his position within the mathematical community.
[4] Indeed, 111 (303 in base 6) and 141 (353 in base 6) are the only palindromes we have in common with the sloths.
